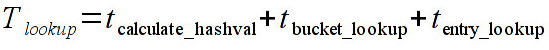One thing that caught my interest lately was the implementation of hash tables, particularly the algorithms we are currently using for calculating the hash value. In kmod we use Paul Hsieh’s hash function, self entitled superfast hash. I fell troubled with anything that entitles itself as super fast, especially given the benchmarks provided are from some years ago, with older CPUs.

After some time spent on benchmarking and researching I realized there were much more things to look after than just the hash function. With this post I try to summarize my findings, showing some numbers. However do take them with a grain of salt.

The hash functions I’m using here for comparisons are: DJB, Murmur32, Paul Hsiesh and CRC32c (using the crc32c instruction present in SSE4.2). My goal is to benchmark hash functions when strings are used as key (though some of the algorithms above can be adpated for blobs). Also the use of these hash tables are only for fast lookups, so any cryptography-safe property of the functions or lack thereof is irrelevant here. For all the benchmarks I’m using depmod’s hash tables. There are 3 hash tables:

1. module names: keys are very small, 2 to 20 chars
2. symbol names: keys are mid-range, 10 to 40 chars
3. module path names: keys are the largest: 10 to \~60 chars

On my benchmarks I identified the following items as important points to look after optmizations:

• Hash functions: how do they spread the items across the table?
• Time to find the bucket
• Time to find the item inside the bucket
• Hash functions: time to calculate the hash value

Whilst the first and the last ones depend on the algorithm chosen for calculating the hash value, the second and third are more related to the data structure used to accommodating the items and the size of the table.

Hash functions: how do they spread the items across the table?

It’s useless to find a hash function that is as fast as it can be if it doesn’t cope with it’s role: spreading the items across the tables. Ideally each bucket would have the same number of items. This ideal is what we call perfect hash, something is possible only if we known a priori all the items and can be accomplished by tools like gperf. If we are instead looking for a generic function that does its best on spreading the items, we need a function like the ones mentioned above: given any random string it calculates a 32 bits hash value used to find the bucket in which the value we are interested in is located. It’s not only desirable that we are able to calculate the hash value very fast, but also that this value can be in fact useful. A naive person could say the function below is a super fast constant time hash function.

uint32_t naive_hashval(const char *key, int keylen)
{
        return 1;
}

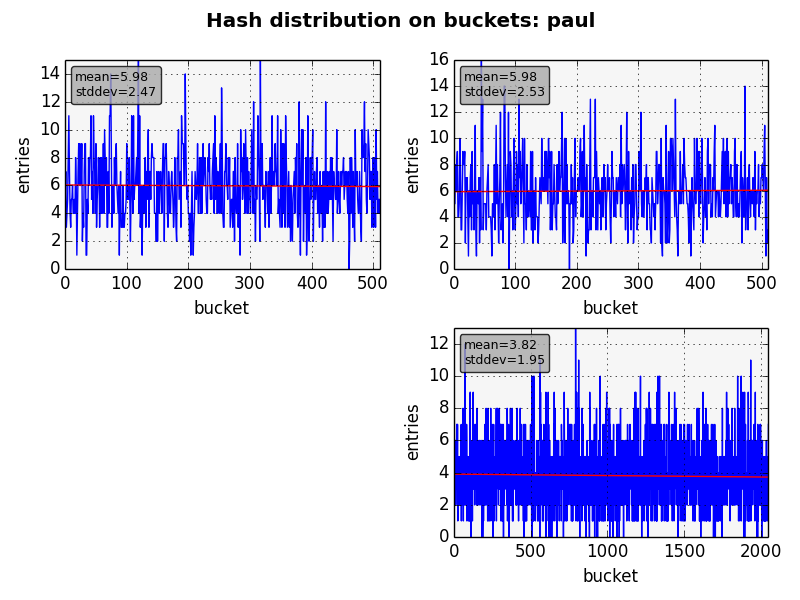
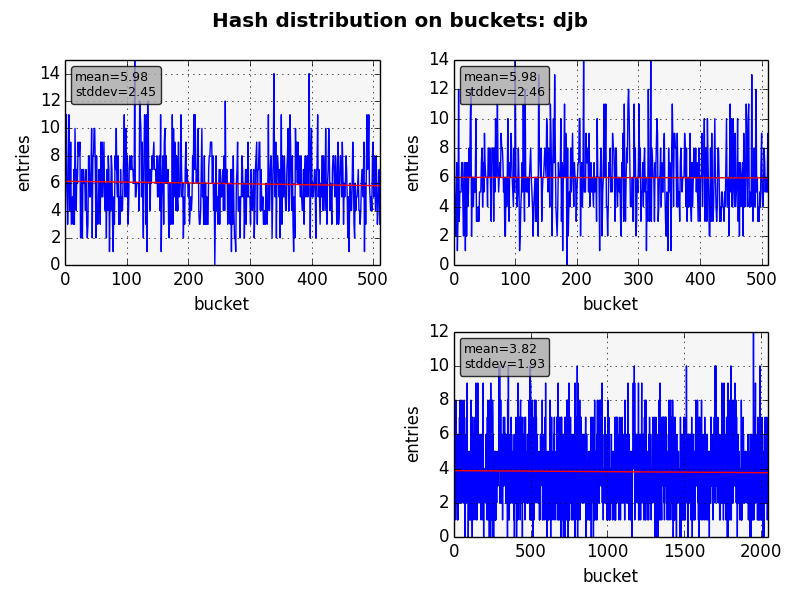
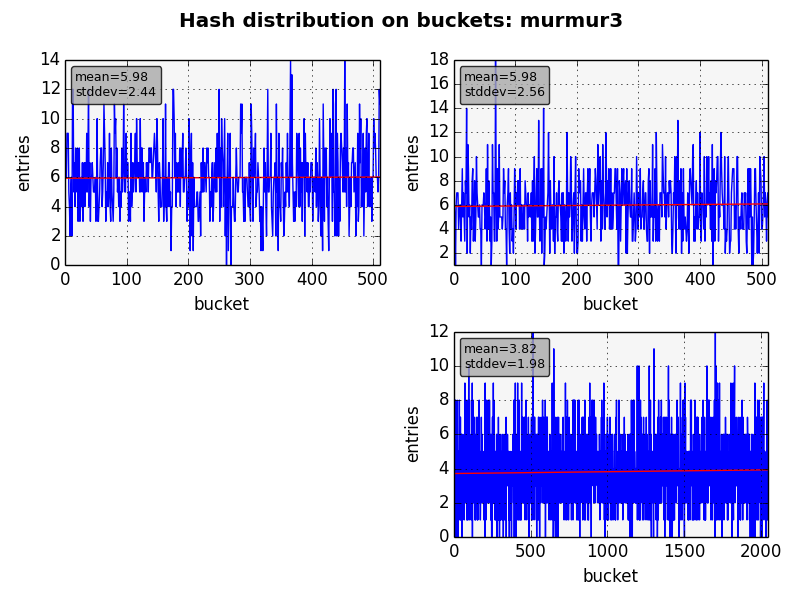
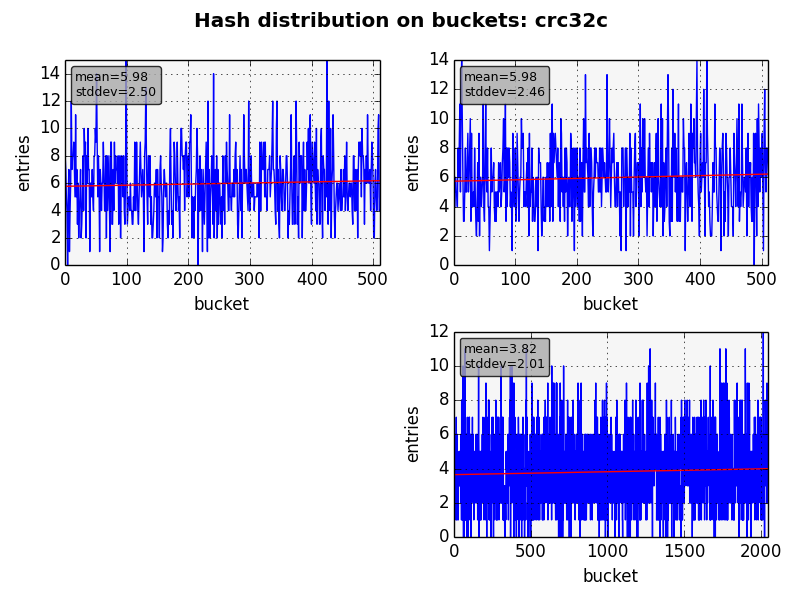
However as one can note it isn’t used anywhere because it fails the very first goal of a hash function: to spread the items on the table. Before starting the benchmarks I’ve read in several places that the crc32c instruction is like the function above (though not that bad) and couldn’t be used as a hash function for real. Using kmod as a test bed this isn’t what I would say. See the figures below.

We used all 3 hash tables used in depmod, dumping all the items just before destroying them. The graph shows how many items were in each bucket. For all algorithms we have almost the same average and standard deviation. So, which functions should we use for the next benchmarks? The answer is clearly all of them since they provide almost the same results, being good contenders.

Time to find the bucket

Once we calculated the hash value, it’s used to find in which bucket the item lies on. For starters, a bucket is nothing more than a row in the table as depicted below:

b0 it1 → it2 → it3 b1 it4 b2 it5 → it6 → it7 → it8 b3 it9 → it10 → it11

The hash table above has size 4, which is also the number of buckets. So we need to find a way to convert the (32-bit) hash value to a 3 bits. The most common way used in hash table implementations is to just take the value’s modulo:

uint32_t hashval = hashfunc(h, key, keylen);
int pos = hashval % h->size;

The size above is set when the hash table is created (some hash table implementations use a grow-able approach, which is not treated in this post). The modulo above is usually implemented by taking the rest of a division which uses a DIV instruction. Even if nowadays this instruction is fast, we can optimize it away if we pay attention to the fact that usually the hash table size is a power of 2. Since kmod’s inception we use size=512 for module names and paths; and size = 2048 for symbols. If size is always a power of 2, we can use the code above to derive the position, which will lead to the same result but much faster.

uint32_t hashval = hashfunc(h, key, keylen);
int pos = hashval & (h->size - 1);

The DEC and AND instructions above are an order of magninute faster than the DIV on today processors. However the compiler is not able to optimize the DIV away and use DEC + AND since it can’t ensure size is power of 2. Using depmod as a test bed we have the following clock cycle measurements for calculating the hash value + finding the bucket in the table:

keylen      before   after
2-10          79.0    61.9 (-21.65%)
11-17         81.0    64.4 (-20.48%)
18-25         90.0    73.2 (-18.69%)
26-32        104.7    87.0 (-16.82%)
33-40        108.4    89.6 (-17.37%)
41-48        111.2    91.9 (-17.38%)
49-55        120.1   102.1 (-15.04%)
56-63        134.4   115.7 (-13.91%)

As expected, the gain is constant regardless of the key length. The time to calculate the hash value varies with the key length, which explains the bigger gains for short keys. In kmod, to ensure the size is power of 2, we round it up in hash_init() to the next multiple with the following function:

static _always_inline_ unsigned int ALIGN_POWER2(unsigned int u)
{
    return 1 << ((sizeof(u) * 8) - __builtin_clz(u - 1));
}

There are other ways to calculate it, refer to kmod’s commit as to why this one is used.

Time to find the item inside the bucket

As noticed in the previous section we use a MOD operation (or a variation thereof) to find the bucket in the table. When there are collisions and
a bucket is storing more than 1 item, hash table implementations usually resort to a linked list or an array to store the items. Then the lookup ends up being:

1. Calculate the hash value
2. Use the hash value to find the bucket
3. Iterate through the items in the bucket comparing the key in order to find the item we are interested in.
4. Return the value stored.

So often the item is a struct like below:

struct hash_entry {
        const char *key;
        void *value;
};

In the struct above I’m considering the key is a string, but it’s also possible to have other types as key.

So once we have the bucket, we need to go through each item and strcmp() the key. In kmod since we use an array to store the items we have a little better approach: the array is kept sorted and during lookup it’s possible to use bsearch(). However as one can imagine, keeping the array sorted doesn’t come for free. We are speeding up lookup with the downside of slowing down insertion.

Thinking on this problem, the following came to mind: we use and benchmark complicated functions that do their best to give a good 32 bits value and then with the modulo operation we use just throw away most of it. What if we could continue using the value? If we don’t mind the extra memory used to store one more value in the struct hash_entry above, we can. We store the hash value of each entry and then compare them when searching inside the bucket. Since comparing uint32 is very fast, there’s no much point in keeping them sorted anymore and we can just iterate very fast through all items in the bucket checking first if the hash values match and only then strcmp() the key. With this we can drastically reduce the amount of string comparisons we do in a lookup-intensive path, the time to add and item (since it doesn’t need to be sorted anymore) and also the complexity of the code. The downside is the memory usage, with one extra 32 bit value for each entry. The table below shows the results.

keylen      before   after
2-10         222.8   127.7 (-42.68%)
11-17        231.2   139.1 (-39.85%)
18-25        273.8   181.3 (-33.78%)
26-32        328.7   236.2 (-28.13%)
33-40        366.0   306.1 (-16.34%)
41-48        354.0   341.7 (-3.48%)
49-55        385.1   390.5 (1.40%)
56-63        405.8   404.9 (-0.21%)

Hash functions: time to calculate the hash value

This was my original intention: to benchmark several hash functions and choose the best one based on data from real world, not random or fabricated strings. My desire was also to profit as much as I could from nowadays processors. So if there’s a new instruction, let’s use it for good.

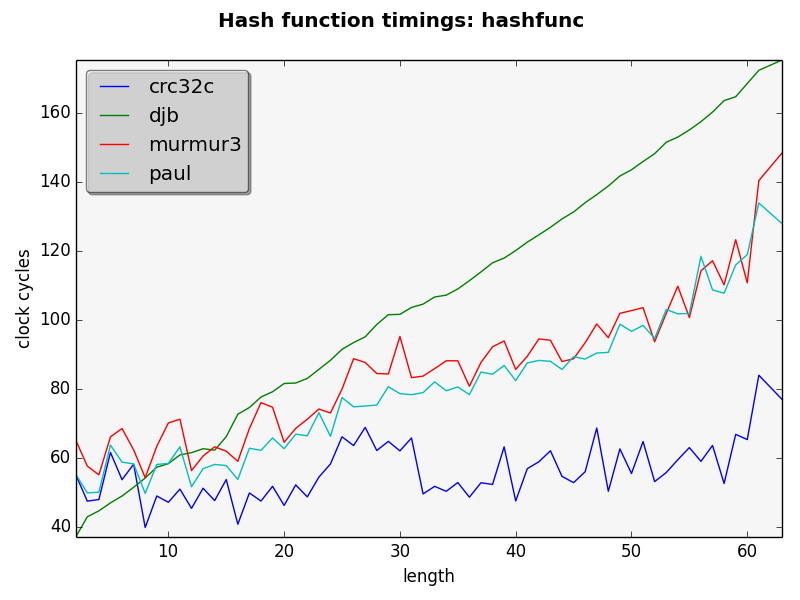
Based on that I came to know the crc32c instruction in SSE4.2. By using it we have a blazing fast way to calculate crc32, capable of a throughput of around 1 char per clock cycle. I was also optimistic about it when I checked that its distribution was as good as the other contenders. The figure below shows the time to calculate the hash value for
each of the algorithms.

As can be seen on the benchmark above, the winner is indeed crc32c. It’s much faster than the others. It’s noteworthy the fact that it increases much less than the other as the length goes up.

From the other contenders, DJB is the worst one reaching much higher times. It’s the simplest one to implement, but in my opinion the others are small enough (though not that simple) to take its place.

How much does the hash function affect the hash table lookup time? By lookup time I mean:

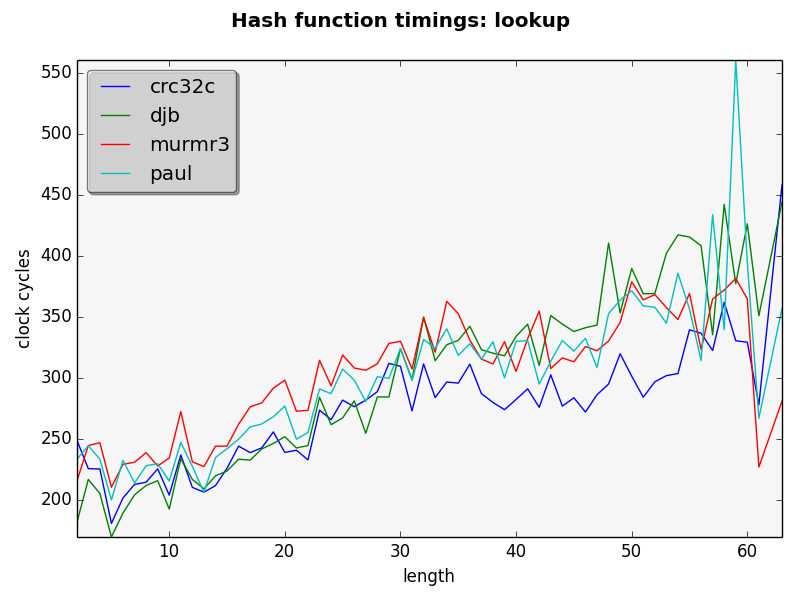
The figure below answers this question:

We can see from the figure above that the crc32 implementation is the faster one. However, the gain is not as big as when we consider only the time to calculate the hash value. This is because the other operations take much more.

Conclusion

Although the CRC32 implementation is faster than its contenders and that I was tempted to change to it in kmod, I’m not really doing it. There would be a significant gain only if the key was big enough. As noted above, the time to calculate the hash value in CRC32 grows much more steadily than the others. If the keys were big enough, like 500 chars, then it could be a change to make. It’s important to note that if we were to change to this hash function we would need to add an implementation for architectures other than x86 as well as introduce the boilerplate code to detect in runtime if there’s support for the crc32c instruction and use the generic implementation otherwise.

The other 2 optimizations, although not ground breaking are easy to make and not intrusive. Nonetheless if people want to check the hash functions in their workload I will make available the code and benchmarks in a repository other than kmod’s.